 打印本文
打印本文  关闭窗口
关闭窗口 关键词: 气候变化; 流域水循环及水资源; 实际蒸散发量; 潜在蒸发量; Budyko 假设
中图分类号: TV213.9 文献标识码: A 文章编号: 1000- 0852(2007)02- 0007- 04
流域的实际蒸散发同时受降水和蒸发能力两个因素控制, Budyko 提出了建立流域水量与能量( 这里主要指由太阳辐射产生的能量) 耦合平衡方程的构想, 即Budyko 假设[1]。许多研究证明了Budyko 假定是成立的, 并根据气象和径流资料拟合了不同流域的水热平衡经验关系式[1- 3]。但是, 已有的研究对证明Budyko 假设的普适性尚不充分, 而且从一个流域拟合的水热平衡经验关系式很难应用到其他流域。因此, 有必要分析不同流域的水热平衡规律并探讨其中的机理。本研究已在黄河流域[4]的63 个子流域验证了基于Budyko 假设的流域水热耦合平衡关系( 式2) , 证明了模型中参数ω~反映流域的地形地貌、土壤和植被等下垫面特征, 并提出了估算ω~的经验公式( 式3) 。为了探讨我国不同地区的水热耦合平衡特征, 并揭示其共同的规律性, 本文将在海河流域和西北内陆河流域( 主要包括疏勒河,黑河,石羊河流域) 进一步验证流域水热耦合平衡模型。
1 流域水热耦合模型
Budyko[1]认为实际蒸散发量与降雨量的比值是降雨与可供能量比值的函数, 即水热平衡方程:

式中: F 假定为适用于所有流域的普适函数。P、E 和Rn分别为流域年降水量、蒸散发量和净辐射量, λ是液态水汽化潜热, 可认为是一常数。在水文学中, 通常采用蒸发能力E0 来代替太阳净辐射Rn, 水面蒸发和参考作物腾发通常被用来代表蒸发能力。根据流域水文气象的物理意义, 我国气候学家傅抱璞[3]在Budyko 假定基础上利用量纲分析和微分方程理论, 推导出了计算实际蒸散发的解析表达式, 如下:
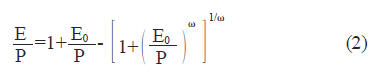
式中ω~为参变量。式( 2) 即为本文采用的流域水热耦合平衡方程。流域的气候特征已反映到方程中P 和E0,其唯一参数ω~则主要反映流域的下垫面特征, 如地形地貌、土壤和植被等。参考前人的研究成果[6][7], 综合考虑坡度, 相对土壤蓄水能力及相对土壤入渗能力的影响, 本研究[4]在探讨黄河流域的水热耦合规律中, 已提出了估算参数ω~的经验公式, 如下:
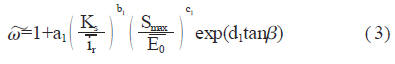
式中: tanβ为流域平均坡度; Smax 为流域土壤最大蓄水能力, 单位为mm; Smax /E0 为将土壤最大蓄水能力无量纲化,即相对土壤蓄水能力; 土壤的饱和导水率(Ks) 控制着降水入渗从而影响着土壤蒸发的供水, 用日平均降水强度( ir ̄) 将饱和导水率无量纲化即可得到相对入渗能力(Ks / ir ̄) 。日平均降水强度为各流域雨天降水量的平均。a1=5.964, b1=- 0.376, c1=0.344 和d1=4.497 是根据黄河流域逐步回归的结果, 本研究继续采用此值。Smax 计算如下:

式中: droot=min ( dTop, dr max) ; dTop 为表层土壤深度; dr max 为最大根层深度; !f 和!w 分别为土壤达到田间持水量和凋萎点的体积含水率, 可根据Van Genuchten 的土壤水分特征曲线公式进行估算, 与田间持水率和凋萎点相应毛管水吸力分别采用为- 340cm 和- 15 300cm 水柱。根据植被类型并参考有关文献给出最大根层深度,表层土壤深度, Van Genuchten 公式所需参数及土壤饱和导水率(Ks) 均来源于FAO 的全球土壤资料[8]。流域的潜在蒸发量E0, 采用Penman-Monteith 公式计算, 如下:
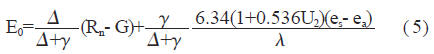
式中: Δ为饱和水汽压- 温度曲线斜率; γ为空气湿度常数; es 为饱和水汽压; ea 为实际水汽压; G 为土壤热通量, 当计算尺度为天或以上时取值为0。太阳辐射是准确估计潜在蒸发量的关键, 一般采用如下经验公式:

式中: Rs 为太阳(短波)辐射; n/N 为相对日照时数; Ra 为大气顶辐射量, 可以由理论公式计算; as, bs 为代表区域气候特征的经验参数, 本文根据收集到的日射站的实测资料进行了拟合。
2 研究采用的资料和方法
在本研究中, 收集了海河流域及其周边54 个、内陆河流域及其周边23 个气象站从1951 到2000 年逐日气象数据, 包括日平均气温、日最高气温和最低气温, 日照时数, 2m 风速, 相对湿度, 日降雨量, 其中有15个站( 海河流域及周边有11 个站) 的同期逐日太阳辐射资料。本研究中收集的资料还包括海河流域内无显著人为影响( 如水库和引水等) 的38 个水文站和内陆河流域( 主要包括疏勒河,黑河,石羊河流域) 7 个水文站自建站至2000 年的逐月径流资料, 以及该流域1km 分辨率的DEM( 数字高程模型) 资料、美国联邦地质调查局(USGS) 的土地利用数据库2.0 版的土地利用图和FAO 全球5km 分辨率的土壤分类和土壤物理参数资料。图1 为本研究中采用的气象站和水文站位置分布。
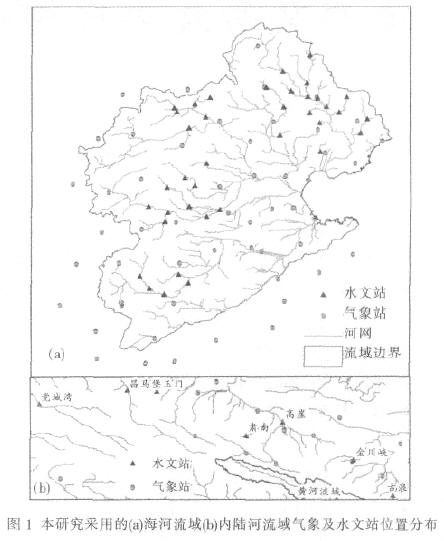
计算流域面平均降水量和潜在蒸发量时, 先将77个气象站的气象要素分别插值到两个流域10km 分辨率的格网上, 按式(5)计算出每个格网的潜在蒸发量,然后统计各子流域的面平均值。除气温外的其他气象要素均按距离方向加权平均法插值, 气温则采用高程修正的距离方向加权平均法插值[9]。在各10km 格网上计算太阳辐射时需要的经验参数as 和bs 取距离最近的日辐射站的拟合值。为了保证流域边界的真实性,先从1km 分辨率的DEM中提取所需要的流域, 转换为10km 格网后再统计流域面平均降水量和潜在蒸发量。利用径流资料计算各个子流域逐年的年径流深,忽略流域储水量的年际变化, 由年水量平衡计算出各子流域的年实际蒸散发量。应该指出, 由于流域储水量的逐年变化, 根据流域年水量平衡计算得到的年实际蒸散发量有一定误差, 但其多年平均是准确的。
为了探讨水热耦合平衡方程式(2)的普适性, 本研究利用多年平均的年降水量、年径流深、年实际蒸散发量和年潜在蒸发量, 对海河流域内38 个子流域,内陆河流域7 个子流域, 由式(2) 拟合出各子流域的参数ω~值并分析其区域分布规律; 本文还对利用下垫面条件估算的经验公式进行了检验, 以说明参数ω~的物理意义。
3 结果和分析
3.1 水热耦合平衡方程中参数的区域分布规律
为了对流域年实际蒸散发量的预测结果进行检验, 本文采用了绝对偏差MEA(Mean absolute error) ,并借用评价径流预报的指标纳西效率系数NSE(Nash- Sutcliffe coefficient of efficiency) 来评价式( 2)对年蒸散发量的模拟精度。在海河流域的38 个子流域和内陆河流域的7 个子流域中, 首先由多年平均的年降水量、年实际蒸散发量和年潜在蒸发量对式( 2) 中的参数ω~进行了拟合。结果表明参数ω~具有显著的区域分布规律, 内陆河流域的ω~值较小, 而海河流域的ω~值较大。表1 中给出了两个流域的ω~值范围, 区域平均值和变差系数CV。内陆河流域( 各水文站的上游区域) ω~均值为1.60, 变化范围为1.32~1.80, 变差系数10.7%; 海河流域的ω~均值为2.95, 变化范围为2.42~4.32, 变差系数为12.9%, 较内陆河流域为大。根据各子流域的拟合参数ω~值, 由式( 2) 对各个子流域逐年的实际蒸散发量进行了模拟计算。以年水量平衡计算的实际蒸散发量作为实测值, 统计模拟误差得到, 内陆河流域7 子流域的纳西效率系数为0.81~0.91; 海河流域38 个子流域的纳西效率系数为0.71~0.97, 其中大于0.9 的有18 个。
为了进一步说明Budyko 假设的正确性, 即式( 2)在海河和内陆河各流域是成立的, 本文还对两个流域的平均参数ω~值进行了检验: 即采用区域平均的ω~值对各个子流域逐年的实际蒸散发量进行了模拟。从表1中的结果可以看到, 在两个区域的模拟精度都稍有降低, 但结果仍然较好。图2 分别给出了石羊河流域的金川峡水文站上游流域和滦河流域的围场水文站上游流域的逐年实际蒸散发量的模拟值与水量平衡计算值的比较。结果表明, 参数ω~不仅具有显著的区域分布特征,而且较好的反映流域的不同水文气候特性。
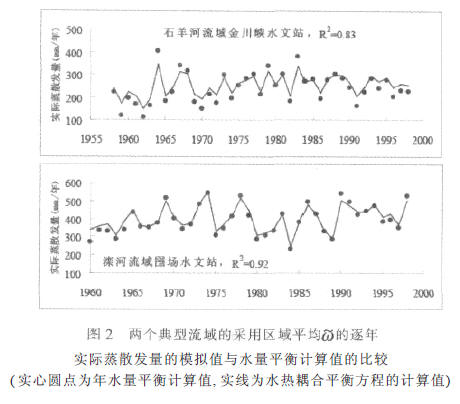
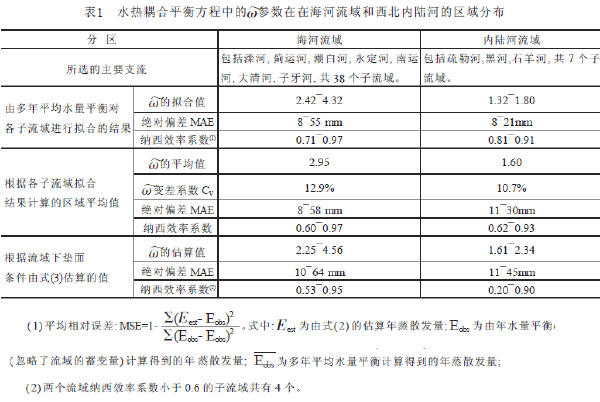
3.2 参数估算方法验证
为了进一步证明参数ω~取决于流域的下垫面条件, 并验证估算参数ω~的经验公式( 式3) 的正确性, 本研究继续采用在黄河流域中得到的参数a1, b1, c1 和d1取值, 对海河和内陆河流域的参数进行了估算。由表1中给出的结果可见, 各个子流域的估算ω~值与拟合ω~值十分吻合。为了检验估算ω~值的准确性, 与前面采用的方法一样, 根据估算的ω~值, 由式( 2) 模拟了各个子流域的逐年实际蒸散发量并与水量平衡结果进行了比较。海河流域的纳西效率系数为0.53~0.95, 纳西效率系数小于0.6 有2 个子流域; 内陆河流域的纳西效率系数0.20~0.90, 纳西效率系数小于0.6 有2 个子流域。在上述4 个计算结果不理想的子流域中, ω~值的计算结果不理想的原因可能与所采用的资料精度有关。结果表明: 经验公式(3)能较好的计算海河流域和内陆河流域的参数ω~,且公式参数在黄河流域、海河流域、内陆河流域共108 个子流域中取值相同, 年蒸发量的估算精度仍然较好。如果采用108 个子流域的结果来回归经验公式( 即式3) 的话, 相应参数变为: a1=8.652,b1=- 0.368, c1=0.436 和d1=- .464。值得注意的是回归结果[4]表明地形坡度的影响是比较小且其与相对入渗能力及相对土壤蓄水能力之间存有一定的相关性, 因此地形坡度与参数ω~的关系不太稳定, 即d1 变化较大, 影响到a1 也有一定程度的变化, 而其他两个主要的影响因素对应的参数则非常稳定。这使得流域水热耦合模型( 式2) 在水文资料不足或无资料地区, 以及评价气候变动对水资源的影响等都具有潜在的应用价值。
4 结语
本文通过对海河流域38 个子流域及内陆河流域
7 个子流域的年降水、径流深及实际蒸发和蒸发能力的分析, 证明了基于Budyko 假设的流域水热耦合平衡关系( 本文中的式2) 是成立的。模型中的参数ω~具有显著的区域分布规律, 在内陆河流域参数ω~的平均值为1.60, 在海河流域参数ω~的平均值为2.95。本文在海河流域和内陆河流域对估算参数ω~的经验公式( 本文中的式3) 进行了验证, 验证的结果较好, 这证明了参数ω~综合反映了流域的下垫面条件, 且式3 能较好计算流域水热耦合平衡模型的唯一参数。流域水热耦合平衡模型对水文资料不足或无资料地区的径流预报,以及评价气候变动对水资源的影响等都具有潜在的应用价值。本研究仍将继续探讨我国湿润地区的水热耦合平衡规律, 以提示其共同的规律性。
参考文献:
[1] Budyko, M. I. Climate and Life [M]. Academic, San Diego, Calif, 1974.
[2] Choudhury, B. J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model [J].J. Hydrol, 1999, 216, 99- 110.
[3] 傅抱璞, 论陆面蒸发的计算[J]. 大气科学, 1981, 5(1), 23- 31.
[4] 孙福宝, 杨大文, 刘志雨等, 基于Budyko 假设的黄河流域水热耦合平衡规律研究[J]. 水利学报, 2007, 38(4), 27- 35.
[5] Zhang, L., K. Hickel, W. R. Dawes, et al. A rational function approach for estimating mean annual evapotranspiration [J]. Water Resour. Res., 2004, 40, W02502, doi:10.1029/2003WR002710.
[6] 谭冠日, 王宇, 方锡林,等。陆面蒸发公式的检验[J]., 气象学报, 1984,42 (2), 231- 237.
[7] 傅抱璞, 山地蒸发的计算[J]. 气象科学, 1996,16 (4), 328~335.
[8] FAO, Digital soil map of the world and derived soil properties, [DB]Land and Water Digital Media Series Rev. 1, 2003.
[9] Yang, D., C. Li, H. Hu, Z. Lei, S. Yang, T. Kusuda, T. Koike, and K.Musiake. Analysis of water resources variability in the Yellow River of China during the last half century using historical data [J]. Water Resour.Res. 2004, 40, W06502, doi:10.1029/2003WR002763.
Validation of Coupled water - energy balance in the Haihe River basin and inland r iver basins
SUN Fu- bao1, YANG Da- wen1, LIU Zhi- yu2, CONG Zhen- tao1, LEI Zhi- dong1
(1. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China;
2. Bureau of Hydrology, Ministry of Water Resources, Beijing 100053, China)
Abstr act: Through the analysis of annual water balance, based on Budyko Hypothesis, a coupled water- energy balance relationship has been established for the Haihe River basin and inland river basins. The unique parameter in the coupled water- energy balance model shows a significant regional pattern. And it has been proved that this model parameter represents the land surface conditions of the studied catchments. At the same time, the present study has proved the empirical relationship (equation 3) for estimating the model parameter from average slope, the relative maximumsoil water holding capacity and the relative infiltration capacity to be of validity in Haihe River basin and inland river basins.
Key words: Climate change, Watershed hydrological cycle and water resources, Actual Evapotranspiration; Potential Evaporation; Budyko Hypothesis
作者简介: 孙福宝( 1980- ) , 男, 河北唐山人, 博士研究生, 主要从事流域水热耦合平衡及水文气候研究。
来源:《水文》2007.04
 打印本文
打印本文  关闭窗口
关闭窗口