一种基于MATLAB的渗透系数确定方法

关键词: MATLAB; 抽水试验; 直线图解法; 配线法

作者：廖梓龙 魏永富 郭中小 贾利民 龙胤慧

中图分类号: TV223．6 文献标识码: A 文章编号: 1672-643X(2012) 02-0175-04

1 概述

导水系数(T) 和渗透系数(K) 是进行地下水资源论证、地下水资源评价和地下水数值模拟的重要水文地质参数[1]。抽水试验法是确定含水层参数的主要方法[2]。

在传统非稳定流抽水试验中，计算渗透系数和导水系数常用的方法有Theis 配线法、Jacob 直线图解法等。不仅如此，目前还有一些改进的优化算法，如全程曲线拟合法[3]、混沌序列法[4]、灵敏度分析法[5]等。计算机有强大的运算能力，因此其技术在含水层水文参数的计算中得到了广泛的应用。国外常用的含水层参数计算软件有AQTESOLV，AquiferTest，Pro 3．5，Aquifer Win32 等，这些软件都是通过建立地下水数值模型进行模拟计算，但它们的使用及计算过程都比较复杂。此外，也有从统计学原理方面进行参数计算的PEST(参数估计和不确定性分析软件) ，但其编程比较复杂。

MATLAB 是矩阵实验室(Matrix Laboratory) 的简称，是美国MathWorks 公司出品的商业数学软件，可用于算法开发、数据可视化、数据分析以及数值计算。采用MATLAB 软件，不仅可以快速进行大量数据的科学计算，还可以克服人工配线过程中产生的人工误差。与其它软件相比，MATLAB 操作比较容易，编程也较简单。本文依据托克托县地下水水源地抽水试验资料，采用MATLAB 优化传统方法中常用的Theis 配线法和Jacob 直线图解法，来计算承压含水层导水系数T 和渗透系数K，这取得了令人满意的结果。

2 抽水试验

2．1 水文地质概况

托克托县境内分布有第三系及第四系砂岩及粉细砂含水层，赋存有潜水和承压水。第四系上更新统及全新统粉细砂含水层，广泛分布于境内，构成浅层水; 一阶平原下部埋藏中、下更新统含水层和二阶平原下部埋藏的第三系含水层构成承压水。

选取托克托县东南丘陵边缘区乃同村附近已有的4 眼井中的3 眼进行抽水试验，由于各井间距均大于500 m(如图1 所示) ，不能满足观测井的布置要求，故采取单孔非稳定流抽水试验。

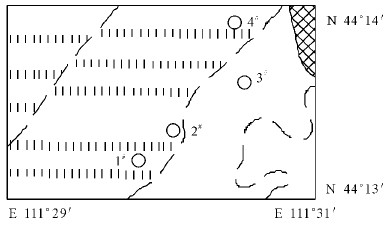
图1 抽水井眼位置简图

查阅现有的水文地质资料后，选取1号井、3号井、4号井作为试验抽水井，各眼井的井深均为150m，过滤管深度为90 ～ 132 m，选取过滤管长度为各井的含水层厚度42 m。

2．2 抽水试验的方法和步骤

采用定流量法，在1号井、3号井、4号井进行单孔非稳定流抽水试验。抽水试验步骤简要概括如下:

(1) 前期准备工作。对所有的抽水孔及其附近有关水点进行水位统测，了解地下水流向，同时要考虑抽出水的排水方案，防止抽出的水回渗。检测仪器设备是否能正常运行。

(2) 进行抽水试验。在抽水开始后第1、3、5、10、20、30、45、60、75、90 min 进行观测，以后每隔30min 观测一次，稳定后延至1h 观测一次。涌水量观测与水位观测同时间同步进行。

(3) 停泵后，观测不同时间段，水位恢复情况，最后，进行抽水试验资料整理及参数计算。

试验从2011 年7 月26 日至7 月30日，共历时5 d，每眼井抽水时间均为1 d。每眼井采用同型号、同功率、同扬程的抽水泵进行抽水，涌水量为40 ～ 68t /h。通过安装在取水管上的流量计读取各取水时间段的抽水量，得到抽水试验过程相应的稳定抽水量，并在相应时间记录井中水位埋深。

2．3 抽水试验成果观测

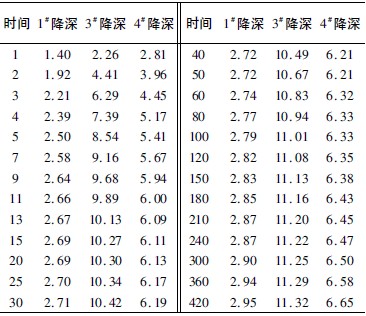
1号井、3号井、4号井在抽水试验进行三小时后，水位趋于平稳，下降幅度减小，最大降深为2．95至11．32 m。选取3 眼井的前28 次观测记录数据进行计算分析。表2 为抽水孔观测数据记录表。

表1 抽水孔观测数据记录表min，m

3 水文地质参数计算

根据1号井、3号井、4号井抽水试验数据计算承压含水层导水系数T 和渗透系数K 。

3．1 基本原理

3．1．1 Jacob 直线图解法

直线图解法的基本思路是将实测数据投在单对数坐标纸上并做成曲线，此实测数据曲线在一定的区间上将呈现为直线，因而可以依据直线的两个要素来确定含水层参数。

当u ≤0．01 时，Theis 公式可以改写成:

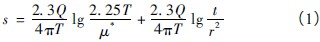
式中: s 为降深，m; Q 为抽水量，m3 /h; T 为含水层的导水系数，m2 /d; t 为抽水时间，h; μ* 为井函数自变量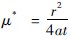，; a 为含水层压力传导系数，L2 /T。

(1) 式表明，s 与lgt 呈线性关系，斜率i 为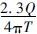利用斜率可以求导水系数T，即:

对于含水层厚度为M 的承压含水层，其渗透系数K:

求解导水系数T 的关键在于确定斜率，因此，首先需要对实测数据进行线性拟合。图2 为基于MATLAB 软件的Jacob 直线图解法框架图。

图2 基于MATLAB 软件的Jacob 直线图解法框架图

polyfit(x，y，n) 在MATLAB 中为用n 阶多项式拟合曲线的命令，因此可以借助它进行曲线拟合。其中， polyfit 为拟合函数命令，x 和y 分别是以向量形式表示的自变量和因变量，n 为n 阶多项式拟合(并非阶次越高，精度亦越高。阶次视具体拟合曲线而定，其输出是从最高次到最低次的系数) 。采用Jacob 直线图解法时，取1 阶多项式(即线性拟合) ，polyfit 输出的系数即为线性拟合的斜率与截距。

3．1．2 标准曲线配线法标准曲线配线法是通过

实测曲线与理论曲线的对比来确定参数的。在对降深及井函数的公式取对数后，可得:

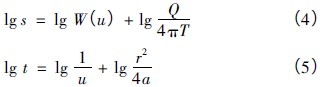
式中: s 为降深，m; Q 为抽水量，m3/h; T 为含水层的导水系数，m2 /d; t 为抽水时间，h; W(u) 为井函数;u 为井函数自变量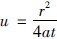，; a 为含水层压力传导系数，L2 /T。

由式(4) 及式(5) 可知，s ～ t 实测曲线与W(u)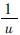～标准曲线在形状上是相同的，只是纵坐标和横坐标分别平移了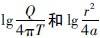的距离而已。只要将二曲线重合，任选一匹配点，记下坐标值带入Theis公式计算即可确定有关参数。

在MATLAB 软件上实现配线法的关键在于坐标的平移[6 －8]。以xa表示t，以ya表示s，以xb表示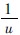以yb表示W(u) ，则实测数据点xa(i) ，(i = 1，2，…，n) 所对应的xb(i) 可以确定:

lgx_a(i) = lgx_b(i) -Δx(i) (6)

则横坐标水平移动的对数值Δx 为:

Δx(i) = lgx_b(i) -lgx_a(i) (7)

同样，每个相对应点上纵坐标移动对数值为:

Δy(i) = lgy_b(i) -lgy_a(i) (8)

每点纵坐标相对平均值的偏差ey(i) 为:

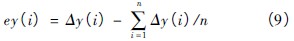
累计偏差EY(i) 为:

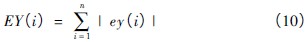
通过MATLAB 编程，选择不同的Δx(i) ，通过程序进行反复比较，使累计偏差达到最小值EYmin，即实现了最佳配线。并输出相对应的匹配点，计算参数。图3 为基于MATLAB 软件的标准曲线配线法框架图。

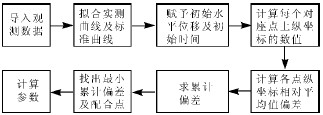
图3 基于MATLAB 软件的标准曲线配线法框架图

在MATLAB 软件中，采用配线法时，同样借助polyfit(x，y，n) 命令进行曲线拟合，取2 阶多项式(即抛物线型拟合) ，同时为拟合好的曲线赋予水平移动坐标的初始值，进行连续迭代，直至找到最小累计偏差，并输出配合点，进行参数计算。使用MATLAB软件优化配线法时，还可以采用其他曲线拟合命令，如幂函数拟合等[9]。

3．2 参数计算

将3 眼井的抽水试验实测数据输入EXCEL 表格，进行整理，再导入已编好的MATALB 程序命令中，即可求得导水系数T 和渗透系数K。表2 为用计算成果表。

表2 计算成果表m2 /d，m/d

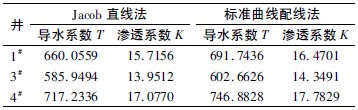
得出的计算结果: 承压含水层渗透系数范围为13．95 ～ 17．78 m/d，导水系数范围为585．95 ～746．88 m2 /d。依据现有水文地质勘察资料及现场调查资料，确定抽水试验区含水层颗粒属于中砂。在查阅水文地质手册进行对比后，计算结果与渗透系数实验室经验值范围10 ～ 25 m/d 及导水系数实验室经验值范围420 ～ 1 050 m2 /d 基本相符合[10]。

4 成果分析

4．1 相关性

渗透系数作为地下水数值模拟中的关键参数，其精确度将直接影响地下水数值模拟的最终结果。在参数检验中，人们常用相关系数来衡量模拟值与实测值的相关密切程度。相关系数越接近于1，表示拟合的效果越好。一般情况下，要求相关系数大于0．8。将MATLAB 法算出的相关系数与EXCEL方法算出的相关系数相比较，发现采用MATLAB 法计算的相关系数均大于0．8。表3 为MATLAB 法与EXCEL 法的相关系数对比。

表3 MATLAB 法与EXCEL 法的相关系数对比

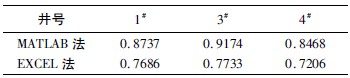
根据表3 的结果可知，采用EXCEL 软件作Jacob直线时，往往带有主观误差，而通过编程实现自动拟合的MATLAB 法则克服了这一误差且相关程度更高。

4．2 精确性

通过MATLAB 的plot(t，s) 命令，其中plot 为二维绘图命令，t 和s 是以向量形式表示的自变量和因变量(时间与降深，绘出降深－历时曲线) 。图4为4号井MATLAB 法的拟合结果。

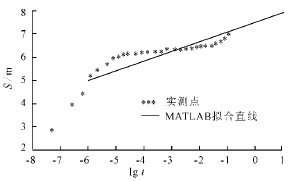
图4 4号井MATLAB 法的拟合结果

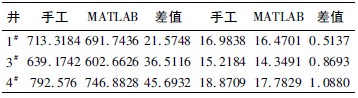
在Jacob 直线法中，拟合直线斜率的改变将直接影响导水系数的取值，因此，只有准确的拟合实测数据，才能获得准确、客观的导水系数值。由图4 可知，MATLAB 法的拟合直线与抽水中后期的实测数据基本吻合。在标准配线法中，MATLAB 法避免了人为的主观性，大大提高了计算结果的精度。表4为手工法与MATLAB 法计算成果对比。

表4 手工法与MATLAB 法计算成果对比

5 结语

(1) 结合托克托县乃同村及其附近一带的抽水试验实例，无论是Jacob 直线法，还是配线法，采用MATLAB 软件编程计算所得的渗透系数及导水系数值，均在实验室经验值的取值范围内，这能真实反映出当地第四系砂岩、粉细砂含水层水文地质条件。

(2) 采用Jacob 直线图解法计算渗透系数及导水系数时，MATLAB 软件法计算的相关系数比传统的EXCEL 法计算的相关系数大，而通过编程实现自动拟合的MATLAB 法克服了这一误差且其相关程度更高。

(3) 采用MATLAB 软件的标准曲线配线法克服了人工主观影响，大大提高了计算结果的精度。

由此可见，基于MATLAB 的Jacob 直线法与配线法是一种计算渗透系数和导水系数的高效、优化方法。

参考文献:

[1]薛禹群，朱学愚．地下水动力学[M]．北京: 地质出版社， 1981， 35(6) : 73 － 77．

[2]康凤新，魏东，张新文，等．大型抽水试验的水文地质意义[J]．水文地质工程地质， 2005， 32(5) : 27 － 30．

[3]肖长来，梁秀娟，崔建铭，等．确定含水层参数的全程曲线拟合法[J]．吉林大学学报(地球科学版) ，2005，35(6) : 73 － 77．

[4]郭建青，李彦，王洪胜，等．确定含水层参数的混沌序列优化算法[J]．中国农村水利水电， 2006(12) : 26 － 29．

[5]刘玉珍，程世迎．灵敏度分析方法确定水文地质参数的基本模型及其应用[J]．水利学报，2006，37 (7) : 846 －850．

[6]朱林子，朱国荣，江思珉，等．Theis 解析模型的数值解及其在Matlab 中的实现[J]．江苏地质，2007，31(3) : 242－ 246．

[7]聂庆林，高广东，轩华山，等．抽水试验确定承压含水层参数方法探讨[J]．水文地质工程地质， 2009， 36(4) : 37－ 40．

[8]朱超群，朱国荣，江思珉．泰斯模型的统计分析求解[J]．水文地质工程地质， 2004， 31(2) : 75 － 78．

[9]李继超，桑有明，邓宇，等．基于MATLAB 的大学生流量与水位降深关系的一种优化计算方法[J]．地下水，2009， 31(2) : 20 － 22．

[10]地质部水文地质工程地质技术方法研究队．水文地质手册[M]．北京: 地质出版社， 1980: 489 － 543．

作者简介: 廖梓龙(1987-) ，男，广西南宁人，硕士研究生，研究方向为水资源管理。