基于分形理论和流域水系分布特征的泥石流研究
摘要:基于MapGIS技术与分形理论,通过计算机编程辅助计算,研究了水系的盒维数值与泥石流各种特征之间的规律。从流域水系的形态及分布特征的角度揭示了流域水系分形维与泥石流危险度之间的深层关系。计算结果分析表明:随着危险等级和特征参数的增加,水系盒维数也呈增长趋势。研究发现通过盒维数的界限值可以界定一条泥石流沟的类型、发育时期和危险程度。其中,分形维1.35和1.42是危险度的界限值,分形维1.34及1.32为泥石流类型和发育期的界限值。
关键词:水系;分形理论;盒维数;泥石流
中图分类号:TV144 文献标识码:A文章编号:0559-9350(2011)03-0351-06
Study on debris flow based on fractal theory and characteristics of water system
ZHANG Chen,CHEN Jian-ping,WANG Qing,ZHANG Wen
Abstract:This paper is trying to describe the characteristics of water system in debris flow drainage basin objectively and accurately so that the debris flow risk level can be determined. Based on the MapGIS and fractal theory,with the aid of computer programming,the relationships between the various features of debris flows and the fractal dimensions of water system are revealed from the view point of morphology and distribution of water system. The results show that along with the increase of the characteristic parameters and the risk level,the fractal dimension of water system exhibits a growing trend. In addition,the threshold values of fractal dimension are found which can be used to define the types, development stages and risk levels of debris flow. It is found that the fractal dimension 1.35 and 1.42 can be taken as the threshold of risk levels of debris flow;and 1.34 and 1.32 can be taken as the threshold of types and development stages of debris flow.
Key words:water system;fractal system;fractal dimension;debris flow
作为研究泥石流危险程度的重要基础,流域水系分布特征成为许多学者研究的对象。张杰林等[1]通过计算水系密度、水系节点密度及优势方位等系统研究了东胜地区地表水系的空间分布规律;李春景等[2]利用GIS软件对流域水系空间分布、河网密度、分歧率、河流弯曲系数等进行了定量分析;杜国云[3]就胶东半岛水系的展布方向、水系分形等水系特征的统计分析,揭示出水系受新构造运动有较明显响应;倪化勇等[4]论述了泥石流流域地貌的分维意义;菊春燕等[5]从分数维方面揭示了吐鲁番市内水系空间分布特征,定性分析了该地区水系网络结构比较简单的原因。在对分形理论的计算机模拟方面,学者们也做了许多工作,陈剑平等[6]在1995年对岩体裂隙网络的分形维进行了计算机的模拟;贾林等[7]在1997年对岩体裂隙网络的多标度性进行了计算机模拟。分形理论在泥石流研究中的应用处于起始阶段,由于这一理论具有对自然界复杂事物进行表达的能力,已逐渐受到大家的关注。其中,关于水系的分数维与其空间分布特征之间的具体规律的研究还较少见,水系形态的分数维到底反映出怎样的泥石流活动特征及危险程度尚无确切的结论[8-9]。本文以金沙江流域的几条典型泥石流水系为例,结合实地考察得到的流域特征参数,在自编的分形程序平台上对这一问题进行研究。
1 理论简介及可行性论证
分形理论由美籍法国数学家B. Mandelbrot提出,研究的是自然界中没有特征长度且有自相似性的图形和现象。流域水系都是主河道中有支河道,支河道中也有自己的支河道,这就呈现出典型的分形结构,所以流域水系完全可以使用分形几何理论进行描述[10]。
泥石流是水系发育到一定程度的必然现象,也是水系进行能量调整的方式,它是在许多因素的共同影响下产生的,这些因素包括主沟床比降,流域切割密度,主沟弯曲系数等。不同的流域水系,在其中发生的泥石流的发育程度、类型及危险程度也必然存在差异,而水系的盒维数也正是由上述因素所决定的[11]。因此,完全可以通过水系的盒维数来表征泥石流的各种特性,即通过水系的盒维数可以了解到该处所爆发的泥石流的多方面的情况。
按照Mandelbrot的定义,分形分布满足如下关系式:

式中:r 为尺度;N 为与r 有关的物体数目;Df为盒维数;C 为常数。
盒维数的测定方法有很多,可以根据研究对象的不同而变化。其中盒维数是应用最为广泛的一种维数。表达式如下所述:

式中:Df为盒维数;Nr (F)为与研究对象相交的正方形个数。
或者也可以表述为是logNr (F)相对于-logr 的斜率值。这里对水系盒维数的测定就是基于盒维数的概念。通过不断对研究区域进行分割,实现动态数方格,进而计算出盒维数。
2 流域水系的盒维数计算
2.1 提取水系原始数据
水系的形态是由各种线段构成的,而这些线段又是由许多的点构成的。为了研究水系的形态,就要将水系线段转化成点坐标提取出来。具体的提取方法如下:将所研究的水系图像导入MapGIS 系统的输入编辑模块,经过矢量化处理,将水系形态转化成MapGIS 中的线文件,经过线拓扑检查将线文件处理成可以导出的文件,由于水系中的某些线段是弧段,为了使程序能够识别出真实的水系形态,还要利用GIS光滑线的功能对水系的线文件进行光滑插值处理,继而通过MapGIS明码文件输出功能最终将水系的形态转化成点坐标的txt格式数据储存起来。这样就完成了计算水系形态盒维数前的数据准备工作。
2.2 计算机编程实现动态数方格
根据分形理论,要计算出水系的盒维数值,就要将研究区域划分为多个方格,而且要不断的变换研究区域内小方格的尺寸,计算出不同尺度下被占用的方格数,将其与尺度指标对应,将数据作于双对数坐标上,方可求出盒维数值。
这样的动态处理过程是人工无法实现的。这里通过Matlab编程自行搭建计算平台实现这一计算过程。在该应用程序中,只要将研究对象的坐标文件导入程序并设置需要将研究区域划分的最多方格数,程序便可通过循环功能自动对区域进行动态分割。假如在窗口设置参数为20,研究区域即可被依次分割成2×2个方格,3×3个方格,4×4个方格,……,20×20个方格,继而程序会将测得的数据绘制于界面的图线框中,并显示出最终计算结果。同时程序还设置有结果数据输出功能,为结果分析提供方便。
为了验证该程序的可靠性,采用文献[9]中的资料,通过MapGIS矢量化处理提取出文献中的曹渡河水系形态数据,使用本程序进行验算,计算得盒维数为1.5389,结果与文中结论基本吻合,说明本程序是合理可靠的。
选取乌东德地区的20条具有代表性的泥石流沟作为研究对象。将这些沟的水系数据文件导入程序计算出每条泥石流沟的水系盒维数值, 并通过文献[8]及《泥石流灾害防治工程勘查规范DZ/T0220-2006》的方法计算出每条沟的危险度等级、泥石流类型和发育期。各危险等级典型泥石流沟的水系分布情况见图1所示,每个水系平均有2万组点坐标数据。程序界面所绘制的图线见图2所示,动态数方格的过程见图3的所示。
图2中的曲线是由lnN(r)和lnr 构成的折线。其中N(r)代表被水系形态占用的小方格的总数目,r代表每个小方格的相对长度,假定研究区域内的小方格总数目为N 个,总面积为S,那么

无标度区间是分形几何中非常重要的指标,水系的无标度区间可以这样判断。图4所示是研究对象中的盐水井和驾车河两条泥石流沟水系的曲线拟合情况。
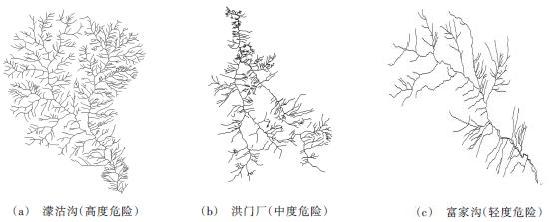
图1 水系
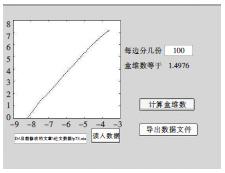
图2 分形程序界面
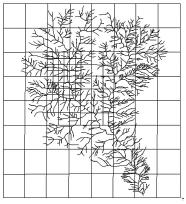
图3 动态数方格
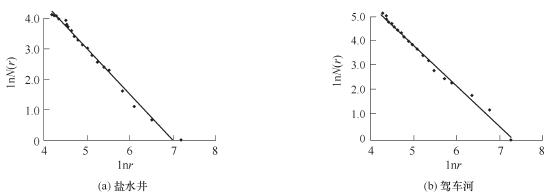
图4 水系图的lnr-lnN(r)曲线
注:r 的单位是m。
从图4可以看出,在lnr>5.2和lnr<4.3时,数据点偏离了直线的范围,而在分形理论中无标度区间正是计算点位于直线范围内的区间, 也就是说lnr<5.2 和lnr>4.3 这一区间, 即小方格的边长r 在e4.3~e5.2m的范围,是该方法计算流域水系空间分布的具有分形维的无标度区间。
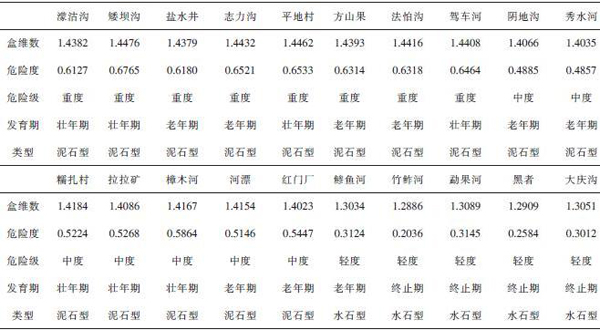
水系盒维数数值及各沟危险度、危险等级、泥石流类型和发育期见表1,其中的水系盒维数与危险度的关系曲线见图5。
表1 水系分维数及泥石流特征描述
3 泥石流特征及水系分布参数与盒维数的关系
首先分析上述20条泥石流沟的水系盒维数与其危险度的直接关系(曲线见图5),继而统计各泥石流沟的水系分布参数:流域切割密度、主沟弯曲系数以及沟床比降,将它们依次与水系盒维数进行比较。其中流域切割密度是流域内水系的总长度与流域面积之比,综合反映了流域内岩石的风化程度,也反映出流域产沙情况及汇流状况;主沟弯曲系数是主沟实际长度与主沟直线长度之比,该指标反映出沟道堵塞难易状况及对泥石流流量的影响状况;沟床比降定义为流域相对高差与主沟长度之比,该指标反映了流域的大小,决定着流域的流程长短以及沿途接纳松散固体物质多少的可能性。水系分布参数与盒维数的分布曲线见图6所示。为了更直观的观察水系的盒维数和泥石流各种特征之间的关系,将危险度、泥石流类型和泥石流发育期的各级别赋值,并做出赋值与盒维数的关系图,具体赋值情况见表2,因为观察到老年期和壮年期的泥石流盒维数没有明显的分界限,壮年期和老年期的泥石流均赋值为2,其中泥石流的各特征值与盒维数的关系见图7。
表2 泥石流各种特征赋值
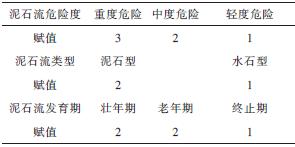
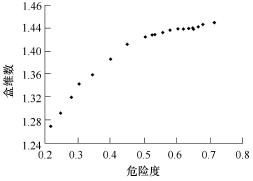
图5 危险度与盒维数关系
4 计算结果分析
从理论上讲,线状对象的盒维数是1,面状对象的盒维数是2。作为水系,其盒维数应该是介于1到2之间的值。从表1可以看出,研究对象的盒维数在1.25到1.5之间,平均盒维数为1.393 8。总体来讲,研究对象呈弯曲状,且结构比较复杂,这从图1的流域水系图中得到了印证。这是因为,从气候条件上看,研究对象所在金沙江河谷属于干热河谷,位于南亚热带及中亚热带,垂直气候变化强烈,其地面温度远大于气温,高温差加剧了岩土体的物理风化作用,谷内日降雨集中,蒸发量大,从而造就了复杂的水系结构。结合图1和表1可以判断,流域水系的盒维数越大,流域的水系结构就越复杂,沟道的弯曲程度就越大。
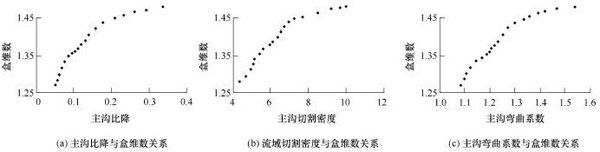
图6 水系特征参数与盒维数关系曲线
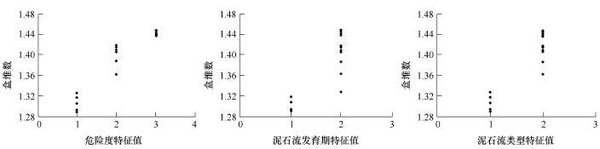
图7 泥石流特征值与盒维数关系
水系盒维数与泥石流危险度的关系方面,从图5可以看出,总体上来说,流域水系盒维数值与对应的泥石流危险度呈正比例关系,且在盒维数达到某个阈值时,泥石流的危险度会较前一阶段急剧增加。
为了讨论出现图5现象的原因,继续做出与水系形态相关的3种危险因子与水系盒维数之间的关系曲线(图6)。从图中的关系曲线可以得知,随着沟床比降、主沟弯曲系数和流域切割密度的增加,水系盒维数呈增长趋势,且当盒维数超过1.35和1.42这两个值时,各个参数的增长速率均比之前有所加快。也就是说,水系盒维数越大,该处山区沟道的比降越大,集水面积越大,流程越长,更加容易接纳沿途的松散固体物质,流域内岩体风化程度越大,沟道较容易堵塞。且当水系盒维数超过一个阈值时,流域内上述特征的演化速度就会提高一个层次,这时更大的主沟床比降和更丰富的支水系为泥石流的运动提供了足够的动能和物源,使得这些沟谷的泥石流相对更加频发,破坏力更大。而图5中曲线中的两个拐点也恰好出现在盒维数值为1.35和1.42的点上,从而证实了上述说法的合理性。另外,如前所述,水系盒维数值与水系分布特征的关系也可以从侧面证实该结论的正确性。
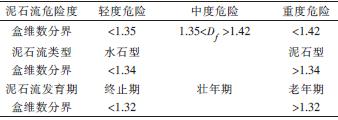
从图7中的各项特征值和盒维数的关系可以看出,水系的盒维数值与泥石流的危险度、发育阶段和类型均存在着明显的分界现象,其具体情况见表3。
表3 盒维数值分界值
5 结论
作者通过自编程序计算出流域水系的盒维数,得出研究区域内各个典型水系的平均盒维数,定量地度量出水系网络的复杂程度。通过对研究对象的切割密度、主沟弯曲系数、沟床比降与水系盒维数关系曲线的分析,并结合实地考察资料,从水系分布特征的角度解释了水系盒维数与泥石流危险度之间的深层规律,并揭示出水系盒维数值与泥石流的各种特征之间的定量关系,找到了鉴别泥石流危险度、泥石流发育期和泥石流类型的盒维数界限值,为分形理论在泥石流评估中的应用和研究提供了参考。
参考文献:
[ 1 ] 张杰林,刘德长,曹代勇. 基于遥感数据融合的水系特征定量化分析方法及其应用[J]. 遥感技术与应用,2004,19(1): 1-4 .
[ 2 ] 李春景. 用Gis 分析流域水系特征—— 以珲春河为例[J]. 延边大学学报(自然科学版),2005,31(4):308-311 .
[ 3 ] 杜国云. 胶东半岛新构造东西分异的水系特征统计分析[J]. 北京大学学报(自然科学版),2001,37(3):407-412 .
[ 4 ] 倪化勇. 泥石流流域地貌形态的统计分形[J]. 水土保持研究,2006,13(6): 92-93 .
[ 5 ] 菊春燕,刘志辉,周绪,等. 干旱、半干旱地区水系空间分布的分形特征及其流域环境的初步探讨[J]水士保持研究,2006,13(3): 174-176.
[ 6 ] 陈剑平,王清,肖树芳,等. 岩体裂隙网络分形维计算机模拟[J]. 工程地质学报,1995,3(3):79—85 .
[ 7 ] 贾林,王士天. 裂隙网络多标度分形计算机模拟[J]. 地质灾害与环境保护,1997,8(3): 48-53 .
[ 8 ] 刘希林,唐川. 泥石流危险性评价[M]. 北京: 科学出版社,1995 .
[ 9 ] 杨太华,苏维箛,何凡峰. 黔南曹渡河流域水系的分形分维研究[J]. 贵州科学,1992,10(1): 61-66 .
[ 10] Yuen Shiu Yin,Chun Ki Fong . Fractal dimension estimation and noise filtering using Hough transforms[J]. Signal Processing,2004,84: 907-917 .
[ 11] 舒安平,费俊祥,刘青泉. 非均质泥流的输移特性[J]. 水利学报,2003(7):46-51 .
作者简介:张晨(1983-),男,天津人,博士生,主要从事边坡工程与地灾防治研究。
|
延伸阅读
|